2025년 11월 28일
안녕하세요! 미적분은 많은 고등학생들이 특히 어려워하고 부담스러워하는 수학 단원이죠. 하지만 미적분은 내신·수능에서 변별력을 만드는 핵심이에요. 그래서 미적분의 중요성부터, 함수의 극한과 미분·적분까지 개념과 공부법을 시리즈로 정리했어요.
미적분 개념정리 1탄 : 미적분 실생활 활용 사례 ↗️
미적분 개념정리 2탄 : 함수의 극한과 함수의 연속 ↗️
미적분 개념정리 3탄 : 미분 정의부터 미분하는 법, 미적분 공부법까지! ↗️
미적분 개념정리 4탄 : 적분의 정의, 적분 개념, 적분하는 법, 미적분 공부법 ↗️
1. 미분의 정의, 미분의 개념, 미분하는 법
이전 2탄 글에서 함수의 극한과 연속을 잘 이해하셨나요? 그렇다면, 이번 3탄 글에서는 본격적으로 미분의 정의, 미분의 개념, 미분하는 법에 대해 알아보도록 할게요. 마지막에는 미분 잘하는 공부법까지 추천하니, 집중해주세요!
마찬가지로 2022 개정 교육과정 수학 미적분1 목차를 기반으로 미분의 개념에 대한 목차를 제공하니, 큰 그림을 먼저 머릿속에 집어넣도록 해요 :)

아래의 설명을 앱에서 편하게 보고 싶다면, 문제풀이 앱 오르조의 ‘오르조 개념 정복’ 개념서를 확인해보세요!
미분 개념 1. 미분계수
1-1. 평균변화율 공식과 평균변화율 정의를 알아볼게요 :

1-2. 미분 계수의 정의를 배워볼게요 :

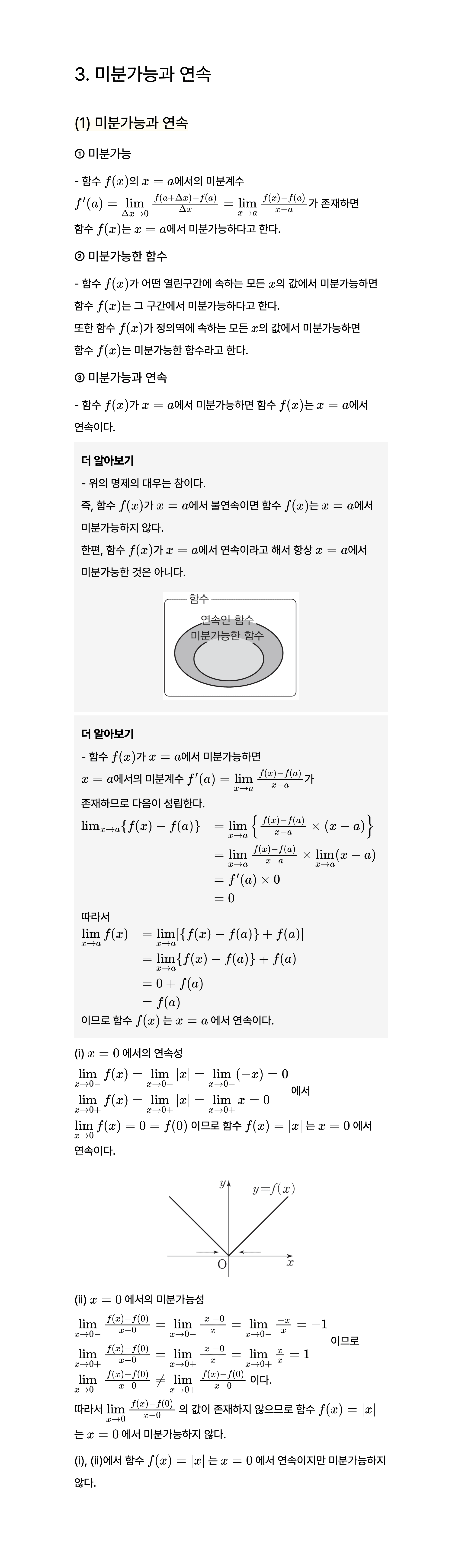
1-3. 미분가능 조건, 미분 가능한 함수, ‘미분가능하면 연속이다’에 대해 알아볼게요 :
미분 개념 2. 도함수
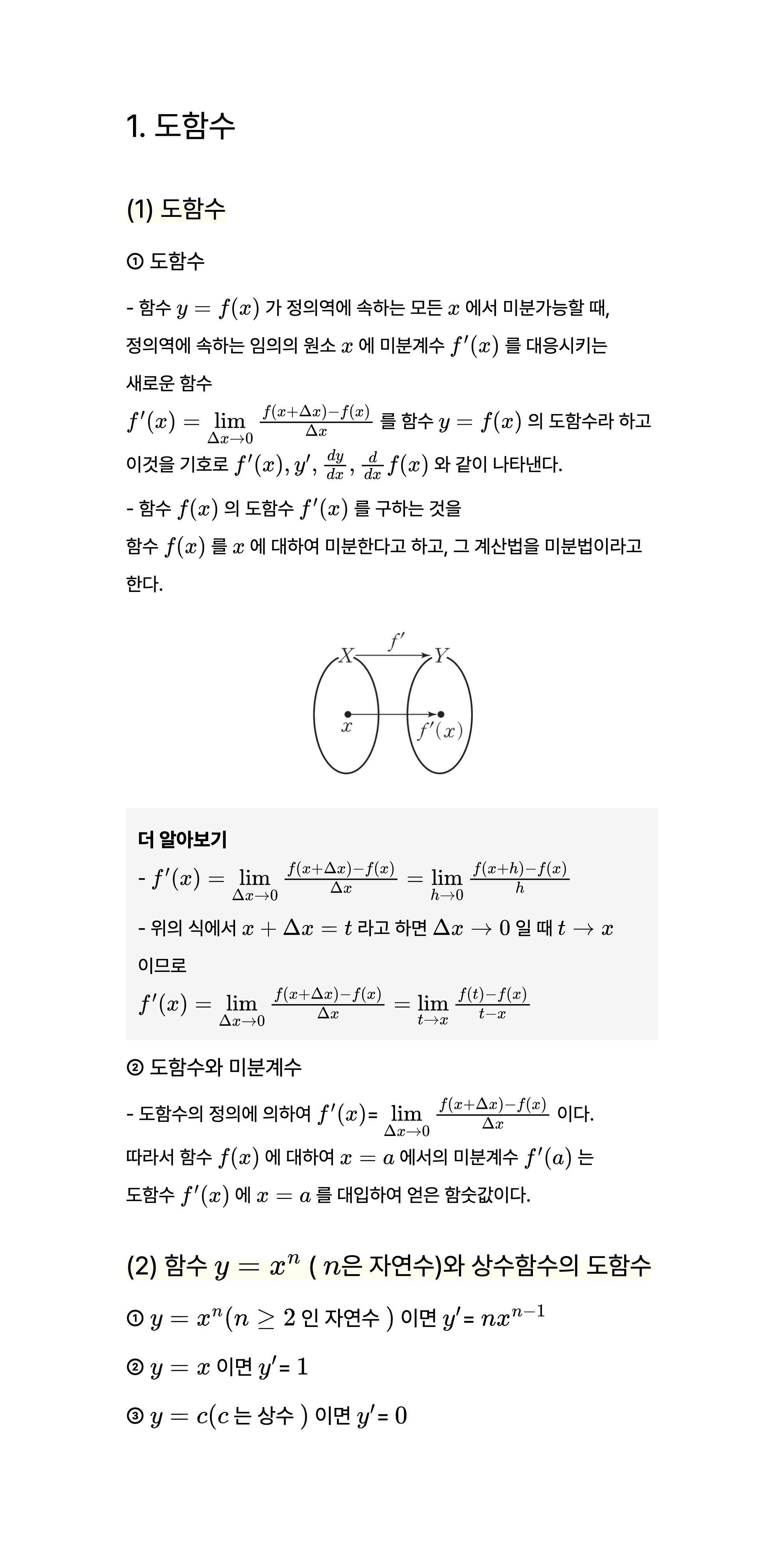
2-1. 도함수의 정의와 도함수 공식을 배워볼게요 :
2-2. 함수의 실수배, 합, 차의 미분법 그리고 곱의 미분법 증명까지 살펴볼게요 :

미분 개념 3. 접선의 방정식
3-1. 접선의 기울기 공식과 접선의 방정식 공식을 알아볼게요 :

3-2. 평균값 정리, 롤의 정리, 평균값 정리 활용을 살펴볼게요 :

미분 개념 4. 함수의 극대 극소와 그래프
4-1. 함수의 증가와 감소를 알아볼게요 :

4-2. 극대극소 정의, 극값의 정의, 극값을 가질 조건을 배워볼게요 :

4-3. 함수의 그래프 그리는 법, 3·4차함수 그래프 개형을 살펴볼게요 :

4-4. 최대 최소 정리와 최댓값 최솟값 구하는 법을 알아볼게요 :

미분 개념 5. 방정식과 부등식
5-1. 실근의 개수, 삼차방정식 근의 판별을 배워볼게요 :

5-2. 위치 속도 가속도 미분에 대해 알아볼게요 :

2. 미적분 잘하는 공부법 - 미분 편
지금까지 미분의 정의, 미분의 개념, 미분하는 법에 대해 함께 알아봤는데요. 개념을 한번 봤으면, 공부는 이제부터 시작이죠. 앞으로 본격적으로 어떻게 공부하면 좋을지 알려드릴게요! (공부법의 큰 틀은 각 편 별로 비슷해요.)
소단원 미분 예제
앞에서 미분의 개념을 한번 본 건 개념서를 한번 훑은 것과 비슷해요. 개념을 처음 봤으니까 예제를 풀어보면서, 미분의 개념을 익히길 추천해요.

모든 소단원 예제를 직접 오르조 앱에서 쓰면서 풀고 싶다면, 오르조 개념 정복 콘텐츠를 이용해봐요!
👉 오르조 개념 정복에서 미분 예제 풀기
대단원 평가
소단원 예제까지 모두 마무리했다면, 대단원 평가를 진행해야 해요.

모든 대단원 평가 문제를 직접 오르조 앱에서 쓰면서 풀고 싶다면, 오르조 개념 정복 콘텐츠를 이용해봐요! 단원 평가 문제는 비교적 쉬운 평가원·교육청 기출 문제로 구성되어 있어서, 미분의 개념을 익히면서 동시에 실전 감각까지 기를 수 있어요.
👉 오르조 개념 정복에서 단원평가 풀기
미분 기출문제 모음 풀이
단원 평가까지 다 풀었으면, 본격적으로 미분 기출문제를 풀어보는 게 좋아요. 반복해서 틀리는 유형의 기출문제가 있다면, 복습을 통해 취약한 개념을 극복하는 게 중요해요.
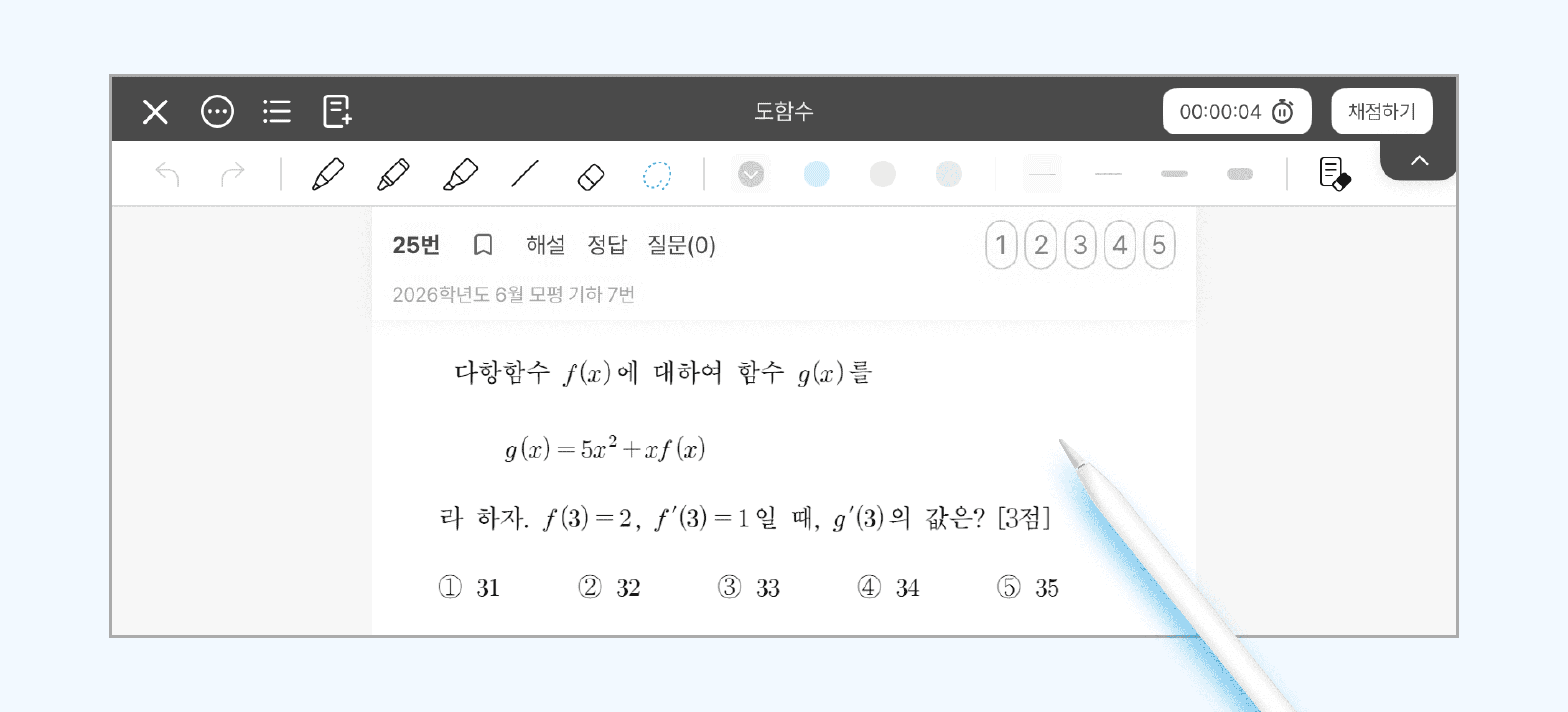
최신 년도까지 유형별로 정리된 미분 기출문제를 오르조 앱에서 직접 쓰면서 풀고 싶다면, 오르조 유형 기출집을 이용해봐요! 취약 유형에 대한 복습 기능까지 지원해요.
👉 오르조 유형 기출집 풀기
미분의 개념 리마인드
개념은 누구나 시간이 지나면서 희미해지기 마련이에요. 잘 기억이 안나거나 미분 기출문제를 풀다가 관련 미분 개념이 궁금해질 때, 개념서 설명을 뒤지지 않고 바로바로 미분의 개념을 질문하고 확인할 수 있으면 베스트겠죠?
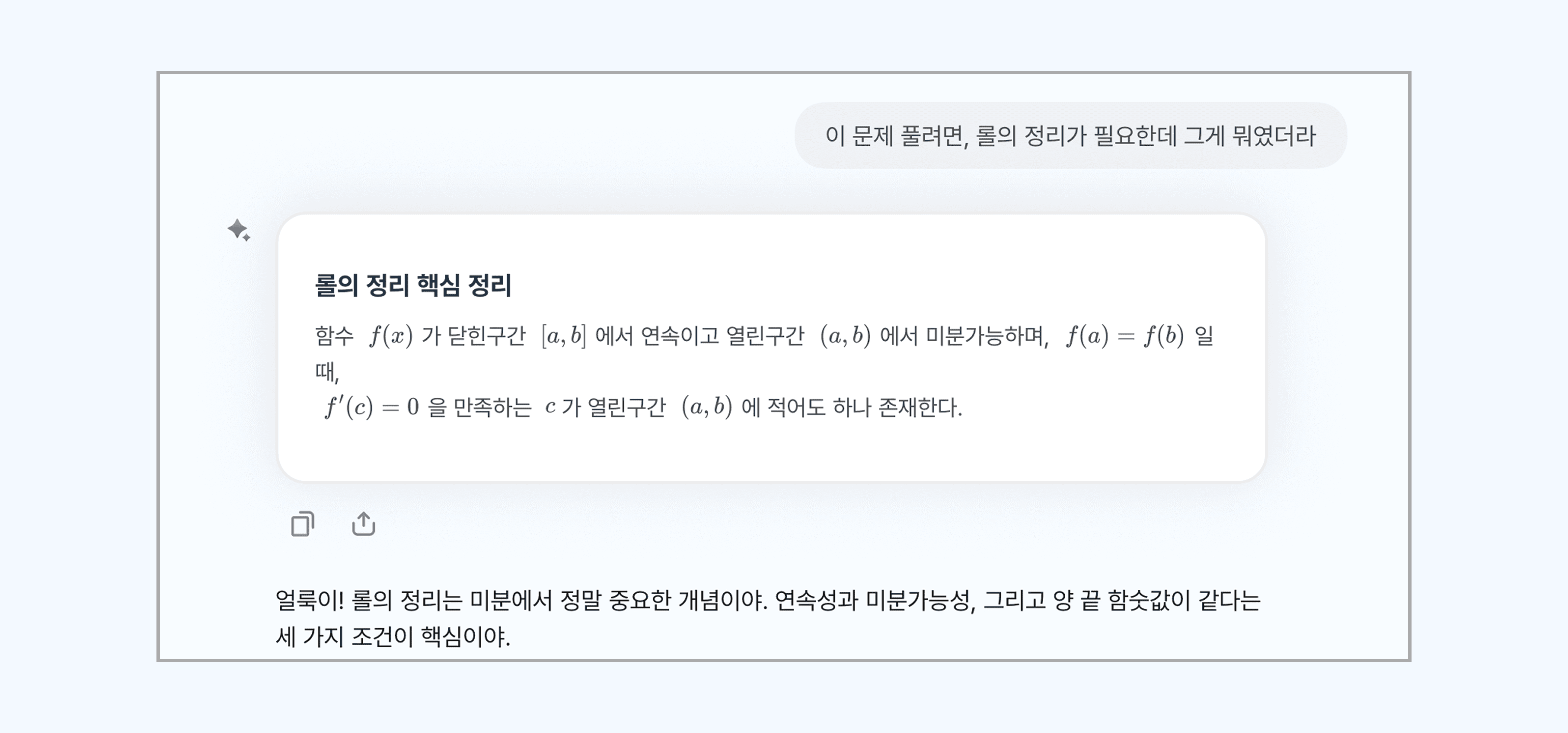
오르조 AI 코치 기능을 통해, 희미해진 미분의 개념을 바로바로 리마인드해봐요!
👉 오르조 AI 코치로 미분 개념 리마인드하기
3. 미분의 개념 및 미적분 공부법 총정리
미분의 정의, 미분의 개념, 미분하는 법
미분은 함수의 한 점에서의 순간 변화율, 즉 접선의 기울기를 구하는 연산이에요.
미분계수는 두 점이 매우 가까워질 때의 극한을 뜻해요.
도함수는 모든 점에서 미분계수를 함수 형태로 나타낸 것이에요.
함수의 실수배, 합, 차, 곱의 미분법 등 다양한 법칙을 통해 계산돼요.
평균값 정리와 롤의 정리는 함수와 접선의 성질을 수학적으로 엄밀히 규명하는 정리에요.
미분을 통해, 순간 변화량을 수학적으로 분석해 함수의 증가와 감소, 극대 극소, 그래프의 형태를 연구할 수 있어요.
미적분 잘하는 공부법 - 미분 편

오르조 앱에서 이 커리큘럼으로 공부하면, 미분의 개념을 완전 정복할 수 있을 거에요. 개념서만 한번 읽고 잊어버리지 말고, 예제와 기출 문제를 풀고 중간중간 개념을 리마인드하면서 정복해봐요!

